A new benchmark to recognize the hardest problems in materials science
By Nicola Nosengo - NCCR MARVEL
Scientists hope that quantum computing will help them study complex phenomena that have so far proven challenging for current computers – including the properties of new and exotic materials. But despite the hype surrounding each new claim of “quantum supremacy”, there is no easy way to say when quantum computers and quantum algorithms have a clear and practical advantage over classical ones.
A large collaboration led by Giuseppe Carleo, a physicist at EPFL and the National Center for Competence in Research NCCR MARVEL, has now introduced a method to compare the performance of different algorithms, both classical and quantum ones, when simulating complex phenomena in condensed matter physics. The new benchmark, called V-score, is described in an article just published in Science.
The study focussed on the “many-body problem”, one of the major challenges in physics. In theory, the laws of quantum mechanics give you everything you need to exactly predict the behavior of particles. But when you have several particles interacting with each other, as it happens in a complex molecules and crystals, this calculation becomes impossible.
A good example of a many-body problem is when physicists and chemists need to calculate the ground state of a material, that is its lowest possible energy level and tells you whether the material can exist in a stable state, or how many different phases it can have. In most cases, scientists must make do with approximating the ground state, rather than calculating an exact solution. There are several techniques and algorithms to approximate the ground state for different classes of materials, or for properties of interest, and their accuracy can vary a lot.
Enter quantum computing. In principle, a quantum system – like the qubits that make up a quantum computer - is the best way to approximate another quantum system, such as the electronic structure of a material, and several algorithms that allow to calculate ground states on quantum computers have been devised. But do they really offer an advantage of classic algorithms, such as Monte Carlo simulations? Answering requires a rigorous and clear metric to compare the performance of existing – or future – algorithms. “Quantum computing is where theoretical computer science and physics meet”, says Carleo. “But computer scientists and physics may have different views on what constitutes a hard problem”. When companies like Google claim to have achieved “quantum supremacy”, an emphatic term that indicates a clear advantage in using quantum computers over classical ones, they often base their claims on solving computational riddles that have no real practical application. “In this article we identify problems that really matter to physics and try to measure how complex they actually are”.
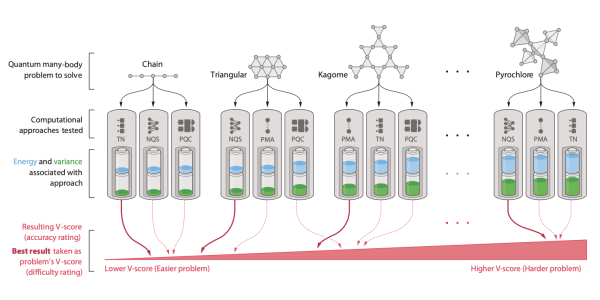
Sketch of the V-score as a metric of simulation hardness. A low V-score is associated with high accuracy. The best result per
Hamiltonian is then taken as the V-score for that Hamiltonian and used to rank the Hamiltonians in terms of simulation accuracy, highlighting which quantum many-body models are hard to simulate with current methods. Image from Wu et al, Science (2024).
Carleo and his colleagues, who come from several institutions in Europe, America and Asia, started by assembling a library of ground state simulations of different physical systems and based on different techniques. They focused on “model Hamiltonians”, that are functions that simplify interesting phenomena found in groups of material, rather than specific chemical compounds. A typical example is the Hubbard model, that is used to simulate superconductivity.
For some of those functions, an exact solution exists – either from very expensive calculations or from experiments – that can be compared with the result obtained from various algorithms, to estimate their error. Based on that, the research team came up with a relatively simple error metric, that they called V-score (or “variational accuracy”), based on a combination of the ground state energy calculated by the algorithm for a given system, and the energy fluctuation. “To have a good description of a material’s ground state we need an estimate of its energy, that must be low enough to allow the system to be stable, and we need to know that energy fluctuations are close to zero, meaning that if you measure the energy of the system several times the remains the same” explains Carleo. “We found that the combined value of energy level and energy variation in a many-body calculation is highly correlated with the error. We validated the metric on materials for which we have the exact solution, and then we used it to estimate the error for the other cases, typically very large systems”.
This way, the group could identify what are the hardest problems in computational materials science, that are hose where no existing method has a low V-score.
The results show that that 1D materials (the class that includes carbon nanotubes) are easily solved by existing classical methods. “This does not mean they are simple problems per se, but that we have good techniques to tackle them” Carleo points out.
Many 2D or 3D materials are also relatively easy. On the other hand, 3D crystal structure made up of many atoms and with “frustrated” geometries – complex arrangements of atoms caused by magnetic interactions – have a high V-scores. The Hubbard model itself, when used on 2-D systems where there is a strong competition between electrons’ interaction and their mobility, proves to be hard for existing methods. These are systems where future quantum computing algorithms may really make a difference.
Carleo explains that the point of the study is not so much to rank existing techniques, but to have a reliable way to assess the advantage brought by new ones that will be introduced. “Our database and codes are fully open access, and we’d like it to become a dynamic resource that is updated whenever a new technique is introduced in the literature”.
Reference
Dian Wu, Riccardo Rossi, Filippo Vicentini, Nikita Astrakhantsev, Federico Becca, Xiaodong Cao, Juan Carrasquilla, Francesco Ferrari, Antoine Georges, Mohamed Hibat-Allah, Masatoshi Imada, Andreas M. Läuchli, Guglielmo Mazzola, Antonio Mezzacapo, Andrew Millis, Javier Robledo Moreno https://orcid.org/0000-0001-6852-7296, Titus Neupert, Yusuke Nomura, Jannes Nys, Olivier Parcollet, Rico Pohle, Imelda Romero, Michael Schmid, J. Maxwell Silvester, Sandro Sorella, Luca F. Tocchio, Lei Wang, Steven R. White, Alexander Wietek, Qi Yang, Yiqi Yang, Shiwei Zhang, and Giuseppe Carleo, "Variational Benchmark for Quantum Many-Body Problems", Science, 386, 6719 (2024). doi: 10.1126/science.adg9774
Low-volume newsletters, targeted to the scientific and industrial communities.
Subscribe to our newsletter