A breakthrough on Weyl semimetals
Fiorien Bonthuis, EPFL, NCCR MARVEL
In their recent paper, Distinct Evolutions of Weyl fermion quasiparticles and Fermi arcs with bulk band topology in Weyl semimetals, two MARVEL groups — led by Prof. Ming Shi and Dr Nan Xu at PSI for the experimental part, and with Prof. Oleg Yazyev and Dr Gabriel Autès at EPFL for the theoretical side — joined forces to shed light (and soft X-rays) on the relationship between the bulk band topology in Weyl semimetals and two measurable signatures of Weyl fermion quasiparticles: magneto-transport effects in the bulk, and Fermi arcs on the surface.
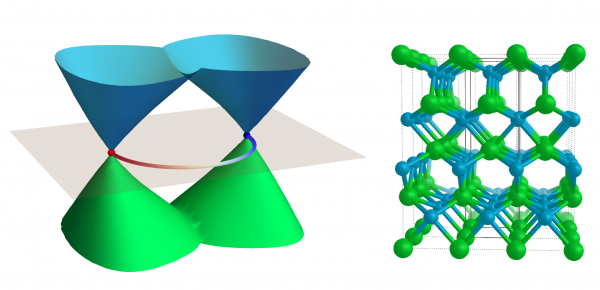
Left: schematic representation of the band structure of a Weyl semimetal in the proximity of two Weyl nodes with opposite chirality. On the surface of the crystal, the projection of the Weyl nodes are connected by a Fermi arc surface state. Right: crystal structure of the Weyl semimetals TaAs, TaP and NbP.
Although Weyl semimetals were experimentally identified only as recently as 2015, their story begins almost a century earlier, with the publication of Dirac’s equation in 1928. Dirac himself proposed a solution to his equation, suggesting in a 1931 paper that it predicted not just the existence of the electron, but also of its counterpart, the positron. Crucially, Dirac suggested the existence of this new fundamental particle purely on the basis of theoretical reasoning: the mathematics of the equation suggested there had to be an ‘anti-electron’, but such a particle wasn’t observed experimentally until a year later. (It was first glimpsed in 1932, by Carl Anderson, who, as it happened, was unaware of Dirac’s prediction.)
At the time, Dirac’s idea that one could predict the existence of a new particle on the basis of theoretical reasoning alone, without prompting or support from experimental results, was seen as extremely bold. However, positrons weren’t the only or even the most experimentally elusive particles predicted purely theoretically on the basis of Dirac’s equation.
In 1929, the mathematician Hermann Weyl proposed an alternative solution to Dirac’s equation. If Dirac had solved the equation for particles with mass, Weyl attempted a solution for particles without mass. He showed that the four-component spinor of Dirac’s equation can be expressed in terms of a coupled system of two two-component spinors. The surprising thing about this formulation is that, while Dirac’s four-component version preserves parity (left-right symmetry), a single two-component spinor does not. In fact, for massless particles, the equations of the two-spinor version decouple, yielding an equation for two particles with opposite chirality. Thus, Weyl predicted the existence of a new fundamental particle that is both massless and chiral: the Weyl fermion.
To date, Weyl fermions have never been observed in vacuum. Theoretically however, we can predict that they could exist as quasiparticles in a material. Specifically, we can imagine materials that have electronic bands without spin degeneracy which cross at pairs of points at the Fermi level. In such materials the low-energy excitations (or quasiparticles) near these crossing points can be described by an equation that is essentially identical to the Weyl equation. To find such a material, we must look for materials with a topologically non-trival electronic band structure, lacking either time-reversal or inversion symmetry. Again, it took a while for experimental results to catch up with the theoretical predictions: the first Weyl semimetals were experimentally identified in 2015. Weyl semimetals opened up an experimental route to a fundamental particle that had so far been encountered in theory only.
Weyl semimetals have two key characteristics, due to the presence of Weyl fermion quasiparticles. First, in the bulk, the chiral anomaly effect associated with Weyl fermions induces a negative longitudinal magneto-resistance. Second, on the surface, Weyl nodes of opposite chirality project Fermi arcs that are protected by the band topology.
So — quasi-particle discovered, experimental signature established, mystery of the Weyl fermion solved? Not so fast. One might think that Fermi arcs on the surface and negative longitudinal magneto-resistance in the bulk always go together as hallmarks of the presence of Weyl fermion quasiparticles. However, it turns out to be more complicated than that: recent research has shown that materials that one would expect to host the Weyl semimetal phase don’t all behave the same with respect to these two key effects.
To figure out what is going on, the MARVEL team used the state-of-the-art VUV- and soft X-ray (SX)- angle-resolved photoemission spectroscopy (ARPES) beamlines at Swiss Light Source, supported by first-principle calculations. To determine the surface and bulk electronic structures, VUV-ARPES, with high energy- and momentum- resolutions, was used to detect the Fermi arcs of the surface states; while SX-ARPES, with its increased bulk sensitivity and out-of-plan momentum resolution, was employed to uncover the Weyl nodes of the bulk states. Still, as Prof. Yazyev points out "The experimental results are very difficult to interpret without the guidance of theory." To recognize the true experimental signatures of Weyl fermion quasiparticles in the measurements, and to understand their evolution, we need to combine experiments with first principle calculations — and that is precisely what the MARVEL team did.
The team looked at three compounds: TaAs, TaP and NbP. While Fermi arcs are observed in all of them, a negative longitudinal magneto-resistance is present in TaAs and TaP but absent in NbP. Combining calculations and experiments, they found two key differences. First, in TaAs and TaP the Fermi arcs terminate exactly at the surface projections of the Weyl nodes, whereas in NbP they don’t. Second, compared to TaAs and TaP, in NbP the energies of the Weyl nodes are relatively far away from the Fermi level. Crucially, this means that the Weyl nodes in NbP (but not in TaAs and TaP) are enclosed by a Fermi surface that is topologically trivial.
Together, these results explain how we can have one signature feature of Weyl fermions without the other, depending on the bulk Fermi surface topology. First, they account for the absence of negative longitudinal magneto resistance in NbP. Due to the fact that its Fermi surface is topologically trivial, chiral excitations cannot occur in NbP. This means that there are simply no Weyl fermion quasiparticles present in the bulk. Consequently, we expect the magneto-transport effects to be absent as well. Second, they offer a unified account of the evolution of Fermi arcs in NbP and TaP. In NbP, the Fermi arcs do not connect exactly to the surface projections of the Weyl nodes at the Fermi energy, whereas in TaP they do. However, if we shift the chemical potential, such that the pair of Weyl nodes are now enclosed by a single topologically trivial Fermi surface, the Fermi arcs do not disappear (even if the Weyl quasiparticles do). That is, Fermi arc surface states manifest over a much larger energy range than Weyl fermion quasiparticles in the bulk (see figure below).
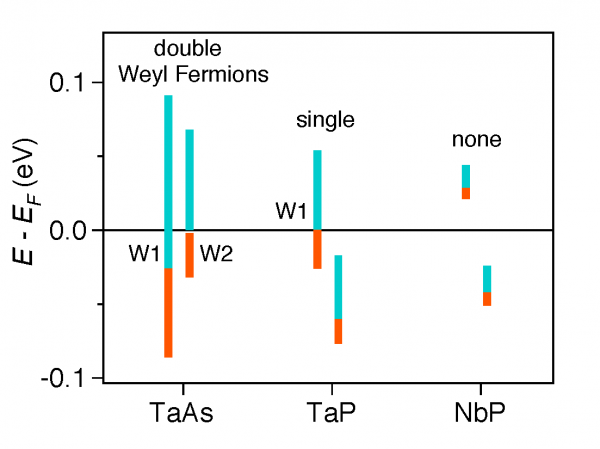
Diagram of the relationship between the energy windows for Weyl fermion quasiparticles and proximity to the Fermi level for TaAs, TaP and NbP. We only get Weyl fermion quasiparticles if there is at least one band crossing point at the Fermi level [0.0] (TaAs, TaP). In this case, we observe both Fermi arcs and negative longitudinal magneto-resistance. We don’t get Weyl fermion quasiparticles if bands cross further away from the Fermi level (NbP). In this case, we don’t get the negative longitudinal magneto-resistance associated with the chiral anomaly effect of Weyl fermions in the bulk, but we do still get Fermi arcs on the surface.
Thus, the MARVEL team arrives at a comprehensive account of the relationship between bulk band topology in Weyl semi-metals and the two signature effects of Weyl fermion quasiparticles, showing that they have distinct evolutions — thereby deepening our understanding of how we can use Weyl semimetals to study Weyl fermions.
This work was a collaboration between researchers at PSI, EFPL, ETHZ in Switzerland and the Chinese Academy of Sciences and Collaborative Innovation Center of Quantum Matter in Beijing.
Reference
N. Xu, G. Autès, C. E. Matt, B. Q. Lv, M. Y. Yao, F. Bisti, V. N. Strocov, D. Gawryluk, E. Pomjakushina, K. Conder, N. C. Plumb, M. Radovic, T. Qian, O. V. Yazyev, J. Mesot, H. Ding, and M. Shi, Distinct Evolutions of Weyl Fermion Quasiparticles and Fermi Arcs with Bulk Band Topology in Weyl Semimetals Physical Review Letters 118, 106406 (2017)
doi: 10.1103/PhysRevLett.118.106406
Low-volume newsletters, targeted to the scientific and industrial communities.
Subscribe to our newsletter