Machine learning and volcano plots: a very 21st century search for the philosopher’s stone
by Fiorien Bonthuis, NCCR MARVEL
It was the magnum opus of medieval alchemy: the search for the Philosopher’s Stone. The elusive substance was the embodiment of the secret of transmutation, of turning one substance into another. Possession of this secret would confer formidable powers: the stone would turn ordinary metals into gold, cure disease, and reveal the mysteries of the body and the soul, of life, death and resurrection. A fanciful amalgam of hands-on experiment and spiritual conjecture, the alchemists’ endeavour was shrouded in secrecy, earning them a reputation as crackpots and charlatans chanting spells over bubbling cauldrons.
Indeed, alchemy today is a byword for pseudoscience — ridiculed as an occult mixture of mercury and metaphor, totally discredited by the scientific revolution. Or…not quite totally. In fact, alchemy wasn’t all fools and knaves. Isaac Newton — who gave us calculus and the theory of gravitation — devoted much of his time to alchemy, writing more than a million words on the subject and taking careful lab notes. Robert Boyle — father of modern chemistry and admired for his rigorous experiments — had a deep and abiding interest in alchemy, replicating and making extensive use of its experimental results. These luminaries of the scientific revolution took the idea of transmutation and the search for the philosopher’s stone quite seriously indeed.
And for good reason: the idea that certain processes can turn a given substance into another substance is absolutely central to chemistry. And so is the insight that such a process can be mediated by an additional substance, which plays an essential part in the process but comes out unchanged. These days, such a substance is known as a catalyst. Catalysts are essential to countless chemical processes, and chemists around the globe are in hot pursuit of the ideal catalyst.
Of course, the search for the ideal catalyst is not simply the search for the philosopher’s stone by another name. 21st Century chemistry is a far cry indeed from its early modern precursor. For one, modern science teaches us that we cannot expect to produce and then multiply gold. For another, it turns out that there is not one universal catalyst, but that every reaction has its own ideal catalyst. So the search is not for a single philosopher’s stone but for a whole heap of philosopher’s pebbles, each one made exactly to fit a given reaction. The game is to find the right pebble for any given reaction.
What you need is a way to rationally design the ideal catalyst for a given reaction: a computational method that tells you, for any given case, which catalysts are the most promising
— Clemence Corminboeuf

This is the problem MARVEL’s Clemence Corminboeuf (Laboratory for computational molecular design at EPFL) and her colleagues have addressed in a series of articles, starting in 2015. “In its full generality, this is a problem you can’t solve experimentally, by tinkering about with different catalysts in a lab — even if you have the most advanced experimental high-throughput set-up,” Corminboeuf says “What you need is a way to rationally design the ideal catalyst for a given reaction: a computational method that tells you, for any given case, which catalysts are the most promising.”
Catalytic reactions can be fiendishly complex, however, and, for all the progress they have made since the 17th century, scientists still often don’t know exactly why or how a catalyst works. With so many factors at play, devising a general computational method to predict the optimal catalyst for any given reaction is prohibitively difficult. One success story stands out: the use of so-called volcano plots, pioneered by Jens Nørskov, to identify the optimal catalyst for heterogeneous and electro-catalytic reactions. Corminboeuf decided to take her cue from this success.
Volcano plots are essentially a graphical representation of the Sabatier principle, which states that the interactions between a catalyst and the reactants should be neither too strong nor too weak: too weak and the catalyst won’t bind to the substrate to start the reaction; too strong and the product won’t dissociate from the catalyst once the reaction is finished. Given this principle, if we take a set of candidate catalysts, and we plot the strength of a catalyst’s interactions on the x-axis against the success of the reaction using that catalyst on the y-axis, we should get a maximum, and a volcano shaped curve. The best catalyst appears at the top of the volcano, defining the ‘just right’ binding strength of the catalyst and the corresponding optimal performance of the reaction; less optimal catalysts appear progressively lower down to the left (binding too strong) and to the right (binding too weak) of this peak.
Given their ability to identify attractive catalysts and their conceptual simplicity, it seemed like an obviously attractive idea to import volcano plots from the heterogeneous community to the realm of homogeneous catalysis.
— Clemence Corminboeuf
Volcano plots are a straightforward enough tool. They are used extensively in heterogeneous catalysis and in electro-catalysis as a simple and effective way to compare the performance of different catalysts for a given reaction. “As a computational tool, volcano plots are very intuitive. They have this great predictive power and a striking simplicity,”Corminboeuf says. “But while they are standard procedure in heterogeneous and electro-catalysis, they remained unused in homogeneous catalysis. So, given their ability to identify attractive catalysts and their conceptual simplicity, it seemed like an obviously attractive idea to import volcano plots from the heterogeneous community to the realm of homogeneous catalysis.”
There were a few obstacles though. Volcano plots were conceived to reflect the thermodynamics of a reaction. For heterogeneous and electro-catalytic reactions this thermodynamics-only approach has been very successful. In these reactions, the catalyst is typically a solid, while the reactants are liquids or gases. Reactants adsorb to active sites on the catalyst’s surface, where the catalytic reaction takes place, after which the products desorb again. In this scenario, the efficiency of the reaction is strongly linked to the thermodynamics of the adsorption/desorption process. But for homogeneous reactions the picture is more complex. In these reactions, the catalyst and the reactants are typically all gases or all liquids in one big mixture. As the catalysts and reactants move around in the mixture, the spatial configuration of the molecules and their interactions with each other change, and this changes the energy profile. These steric effects interfere with the simple thermodynamics of the coupling and uncoupling of the catalyst. Consequently, the kinetics of the reaction need to be taken into account alongside the thermodynamics, and the success of homogeneous catalysts tends to depend on the interplay between the two. Needless to say, this complicates the analysis enormously.
Undaunted, Corminboeuf, together with Michael Busch and Matthew Wodrich, set about trying to make volcano plots work for homogeneous catalysis. To show that the technique can be translated to this class of reactions at all, they needed to establish a few technical preliminaries. First of all, they needed to demonstrate the existence of linear free energy scaling relationships (LFESRs) between the different steps of the catalytic cycle. This is critical because it proves that the energies of the different intermediates don’t vary independently: this makes it possible to calculate the values associated with an entire catalytic process using a single ‘descriptor variable’. A descriptor is an (experimentally and computationally accessible) parameter that describes the strength of the catalyst/reactant interaction. For instance, heat of adsorption or binding energy for some intermediate would be obvious choices for descriptors. The genius of volcano plots is that, given the LFESRs for a reaction, we only need to determine the values of a suitable descriptor variable to analyse catalytic performance, and to identify the optimal catalyst using the volcano plot.
The first paper on volcano plots the group published, then, was a proof-of-principle study for the Suzuki cross-coupling reaction for olefins. The authors constructed a thermodynamics-only volcano plot for this reaction. They demonstrated the existence of LFESRs and showed that a volcano plot constructed from these could distinguish between different catalysts and reproduce experimentally known trends. This was encouraging, but of course, for homogeneous catalysis a thermodynamics-only plot tells only half the story.
So the next step was to include kinetics and other complexities of homogeneous reactions. The other option, the authors point out, is to initially ignore kinetics and any other factors, and simply use the thermodynamics-only volcano plots as ‘best case scenarios’ for homogeneous catalysis: catalysts that perform well still need a further, full analysis of their kinetics to determine their real promise; by contrast, catalysts that perform poorly can be safely dismissed, as even the most favourable kinetics won’t be able to redeem their thermodynamic shortcomings. From a scientific point of view however, that is a bit unsatisfactory, so in a series of subsequent papers, the authors went on to explore ways of incorporating kinetics and other factors: in one, they supplement the thermodynamic volcano plot with a kinetic version, constructed analogously to the thermodynamic one; in another, they stick to a thermodynamics-only approach but construct a 3D volcano plot to include an additional parameter for cases where some external factor might influence the performance of the catalyst.
One might note, however, that these ideas often entail including an additional descriptor variable. And that happens to be the most costly step in the whole process. It is not just that we have to identify a suitable descriptor (for which there is no recipe; finding a descriptor requires insight and careful study of the underlying reaction mechanism). It is, above all, that descriptor values are usually calculated from first principles DFT (density functional theory) simulations and stored in a large property database. This is an enormously time consuming and expensive process. Indeed, as the number of possible catalysts is sheer endless, calculating all the descriptors by brute force DFT screening is a computational nightmare.
This collaboration really shows the strength of MARVEL, combining different computational competencies to work on issues that are not only of theoretical but certainly also of practical interest. Easy discovery of new and better catalysts is critical to today’s industry, and this research contributes to that goal.
— Clemence Corminboeuf
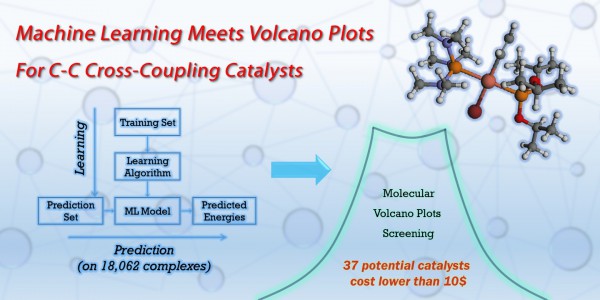
To address this issue of computational efficiency, Corminboeuf’s group teamed up with another MARVEL group, of Anatole von Lilienfeld. In a joint paper, they show how quantum machine learning models can be harnessed to tackle a catalyst screening, by increasing the speed at which the descriptor variable can be determined. Quantum machine learning models can be trained on a relatively small set of potential catalysts for which the descriptor values have been determined using DFT calculations. The trick with machine learning is that it is able to pick up complex correlations between the DFT results and structural properties of the catalyst. It can then use these correlations to make powerful predictions on new structures at a fraction of the computational cost. To test their method, the researchers constructed a thermodynamics-only volcano plot for the Suzuki cross-coupling reaction, and constructed a library of 25116 potential catalysts (or metal-ligand combinations). Starting from a training set of 7054 reaction energy values, they made out-of-sample predictions on the remaining 18062 complexes, identifying 557 catalysts (including 37 with a cost lower than $10) with promising thermodynamic profiles — including both well-known and less expected possible catalysts.
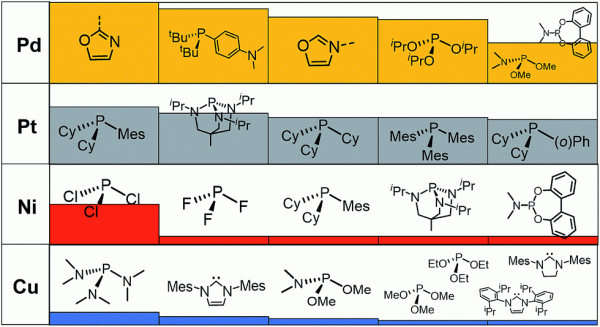
Histogram ranking of the five most identified ligands that appear on the volcano plateau (i.e., with descriptor values between −32.1 and −23.0 kcal mol−1) by metal type as predicted by the machine learning model using the BoB representation. The histogram is scaled relative to the Pd/oxazole ligand combination, which has the highest metal/ligand occurrence appearing 38 times on the volcano plateau. Fig. 6 in DOI: 10.1039/c8sc01949e

“This collaboration really shows the strength of MARVEL, combining different computational competencies to work on issues that are not only of theoretical but certainly also of practical interest. Easy discovery of new and better catalysts is critical to today’s industry, and this research contributes to that goal,” Corminboeuf says. Next to Boyle’s notion that the philosopher’s stone might offer him a glimpse of God’s mysteries, that may sound like a decidedly prosaic goal. Sic transit gloria mundi? Who can tell. Modern catalysts may not have given us gold or eternal life, but they have given us polyethylene and fertiliser — and you never know what these quantum-machine-learning powered volcano plots might yield.
References
B. Meyer, B. Sawatlon, S. Heinen, O. A. von Lilienfeld, C. Corminboeuf, Machine learning meets volcano plots: computational discovery of cross-coupling catalysts, Chem.Sci (2018) Advance Article. DOI: 10.1039/c8sc01949e
M.D. Wodrich, B. Sawatlon, M. Busch, C. Corminboeuf, On the generality of molecular volcano plots, ChemCatChem 10, 1586 (2018). DOI: 10.1002/cctc.201701709
M. Busch, M.D. Wodrich, C. Corminboeuf, A generalized picture of C-C cross-coupling, ACS Catal 7, 5643 (2017) DOI: 10.1021/acscatal.7b01415
M.D. Wodrich, M. Busch, C. Corminboeuf, Accessing and predicting the kinetic profiles of homogeneous catalysts from volcano plots. Chem.Sci 7, 5723 (2016), DOI: 10.1039/c6sc01660j
M. Busch, M.D. Wodrich, C. Corminboeuf, Linear scaling relationships and volcano plots in homogeneous catalysis — revisiting the Suzuki reaction, Chem.Sci 6, 6754 (2015). DOI: 10.1039/c5sc02910d
Contact
Clemence Corminboeuf: clemence.corminboeuf@epfl.ch
Laboratory for computational molecular design, ISIC, EPFL, CH-1015 Lausanne Switzerland
Low-volume newsletters, targeted to the scientific and industrial communities.
Subscribe to our newsletter