Enhancing disorder to create order
by Fiorien Bonthuis, NCCR MARVEL
On June 24th 1812, Napoleon invaded Russia. In true 19th century fashion, his Grande Armée went to war in the most astonishingly colourful and ornate uniforms, with elaborate regimental colours, plumes, sashes, and lots of shiny buttons. In September, Napoleon took Moscow, but he was forced to retreat just a month later. It was October 19th, and winter was setting in. For the French army, wholly unprepared for the freezing conditions, the retreat was a disaster. The Russian winter mercilessly and utterly destroyed Napoleon’s Grande Armée. Destroyed, right down to the buttons of their uniforms, or so the story goes. Those buttons were mostly made out of tin. And at low temperatures, the shape of tin crystals changes, going from a structure that is malleable and metallic to one that is non-metallic and brittle. As the army retreated in the freezing cold, this would have turned the proud, silvery buttons on the soldiers’ uniforms into dull, grey dust.
In a recent paper, MARVEL researchers Pablo Piaggi and Michele Parrinello set out, maybe not exactly to solve Napoleon’s haberdashery woes, but to understand the phenomenon underlying them: polymorphism.
For, whatever the historical accuracy of the story, there’s chemical truth in it. Polymorphism is a substance’s ability to crystallise into different structures. Those different crystal structures, called polymorphs, often have very different properties. This is true for tin, which in one crystal form is good for making buttons, in the other, not so much. It is true for carbon, which in one of its crystal forms appears as graphite and in another as diamond. It is also true, disconcertingly, for almost all active molecules used in pharmaceuticals: a formulation with the exact same chemical composition can be an effective drug in one crystal form, but useless or even toxic in another.
Considering how it can unexpectedly screw up almost anything, from Napoleon’s military campaign to your medical treatment, it’d be nice to be able to control polymorphism: to have a way to predict whether a substance has polymorphs, and if so, which polymorphs form under which conditions.

Polymorphism is a tricky phenomenon, though. In some cases, the slightest change in crystallisation conditions results in the formation of a different polymorph; in other cases, crystallisation robustly and sometimes frustratingly keeps yielding the same polymorph. In some cases, one polymorph slowly or suddenly transforms into another over time; in other cases this never happens without considerable effort, even when the other polymorph is the more stable one.
We can begin to understand this behaviour when we consider that, technically speaking, polymorphism is a matter of a substance having more than one (meta)stable solid state. If we think about crystallisation as, essentially, a process of molecules arranging themselves into some neat, periodic order, it is easy to imagine that there is usually more than one way to do this, and that not all possible configurations will be equally stable. The system will generally tend to the configuration with the lowest free energy. However, given the complexity of the different interacting forces in most systems, it isn’t always a smooth glide straight down to that lowest-energy configuration, and the system may end up in configurations that are local energy minima rather than the absolute minimum. To get out of such a minimum, the system has to cross a high energy barrier. Unless and until it gets pushed over that barrier, the system will stay where it is. That is, the system is in a metastable state and the scenario looks something like Fig. 1.
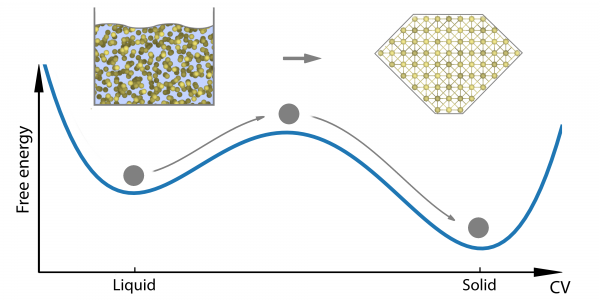
Figure 1. A system with two metastable states.
To control polymorphism, then, we have to figure out where the local minima corresponding to any polymorphs are, and what the barriers between them are like. If we know that, we can predict which polymorph might appear under which conditions.
How would one go about this? The traditional way is to just do a lot of experiments: let the compound in question crystallise under as many different conditions as possible and see if a new crystal structure emerges. The trouble with experimental screening is that it is an expensive, laborious process, and only as exhaustive as time and money permit. In fact, as Prof. Parrinello and Mr Piaggi note in their paper, “experiments can only provide a limited insight into this phenomenon, [so] already in the very early days of computer simulation, much effort has been devoted to the study of crystal nucleation.”
Crystallisation, they continue, is “a remarkable physical process” in which “rare but crucial fluctuations lead to the formation of a solid phase starting from the liquid”. For computer simulations, the trouble comes with the ‘rare but crucial fluctuations’ part: it means that in most cases the time scale of crystal nucleation is much longer than what can be reached in atomistic simulations.
Here’s why: The basic idea of atomistic simulations (of the Molecular Dynamics variety) is very simple: start with a system of atoms; calculate the forces acting on each atom; given those forces and using Newton’s laws of motion, calculate the movement of each atom over a fixed period of time. Adjust the positions of the atoms accordingly. Repeat.
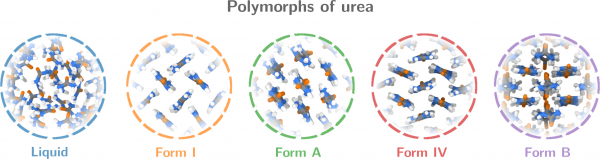
Figure 2. Polymorphs of urea. Form B is a newly predicted polymorph that is stabilised by strong entropic effects (cf. Video 2)
The problem is, enormous gains in computing power over the past decades notwithstanding, the timescales that can be reached with atomistic simulations are still severely limited. This timescale limitation is intrinsic to Molecular Dynamics, Prof. Parrinello explains: to correctly integrate the equations of motion, the time step used to discretise the time evolution must be smaller than the fastest motion in the system, generally a couple of femtoseconds (10-15 seconds). Taking into account the computational cost per step, and the size of the system, this restricts the timescale of a typical MD simulation to microseconds (10-6 seconds, or billions of MD steps.
However, much longer timescales are needed for processes like crystallisation, where the scenario looks as in Fig. 1, and the system has to cross a high energy barrier to go from one metastable state to another. This will happen only under very favourable circumstances, and those circumstances don’t occur too frequently. (In fact, the statistical likelihood of the relevant favourable circumstances occurring decreases exponentially as the height of the barrier increases.)
The transition between one state and another thus becomes a rare event taking place on a much longer timescale than one can simulate in practice.
— Michele Parrinello
“The transition between one state and another thus becomes a rare event taking place on a much longer timescale than one can simulate in practice,” Prof. Parrinello says. “This limitation becomes even more restrictive if one takes into account that a single transition event has only limited value, and one would need to observe many transition events to obtain meaningful statistics.”
Trying to capture those transitions within the timescale of an atomistic simulation is like taking a split-second look at a system in hopes of witnessing an event that happens every once in a while on a timescale that is about a million times longer. What are the chances of that rare event happening in precisely the very short window of your simulation? And of it happening again in your next simulation? Almost zero. To make atomistic simulations work for scenarios like Fig. 1, you have to help the system escape from free-energy minima, or you’ll sit around waiting forever.
Enter Metadynamics, an enhanced sampling method developed by Prof. Parrinello (and, he stresses, many colleagues over the years since the method was introduced in [Laio and Parrinello, 2002]). In essence, the idea is to artificially push up the free energy so as to lift the system out of the free energy minimum and over the barrier. This is done by adding a history-dependent bias potential as a function of the collective variables against which the free energy is calculated. Whenever the system finds itself trapped in a free energy minimum, this bias pushes the free energy up, with each step making the free energy valley less shallow, until it draws even with the top of the barrier, at which point the system drops over the edge into the next free energy minimum, and the whole process starts again.

Thus, instead of waiting, simulation after simulation, for one of those rare fluctuations that would make the system jump over the barrier, Metadynamics effectively helps the system scale the barrier step by step, all within the simulation’s timescale.
From this, we can construct the system’s free energy surface: it is exactly the negative of the bias potential. “With an appropriate choice of collective variables, the free energy surface contains all the relevant information about the system, such as the location and the relative stability of the metastable states and the free energy barriers separating them,” Prof. Parrinello says.
That’s the idea. To make it work for a particular problem — crystal formation, in this case — we must, first of all, make this ‘appropriate choice of collective variables’. This may come as a bit of a surprise: how did we set out to calculate the free energy as a function of a set of variables without knowing what those variables are supposed to be? It is not as daft as it sounds, really.
This shows that, counterintuitive as it may be, entropy can be a crucial stabilising factor, even in crystals.
— Pablo Piaggi
As a matter of fact, free energy cannot be computed directly in atomistic simulations: it would require numerically integrating over all the possible positions of all the particles in the system, and for systems of more than a handful of particles, that’s such an astronomically large, high-dimensional space that even if we managed to perform the calculation, the numerical error would be so large as to render the result useless anyway.
To avoid this gigantic integral, Metadynamics employs a common tactic and reduces the dimensionality of the problem, representing the system in terms of a limited number of parameters, or collective variables (CVs). CVs are functions of the atomic coordinates; they can represent any ‘interesting’ degree of freedom by which different states of the system can be distinguished.
Now, the choice of collective variables is not settled a priori: it’s up to the researcher to decide, through trial and error and rational insight, which CVs to use for a given system. The choice matters a great deal, Prof. Parrinello stresses. This is not because metadynamics won’t work with the wrong CVs. In fact, metadynamics is in principle independent of the exact choice of CV: a non-optimal choice can make for an excessively and unnecessarily long computation time, but mathematically things will work out just fine whatever one’s choice of CVs. No — what’s at stake is not just computational efficiency but explanatory value.
“The choice of CVs is deeply connected to the very idea of metadynamics: enhance the rare but crucial fluctuations that make it possible for a system to move from one metastable state to another. The question is, what are the important fluctuations we need to enhance?” Prof. Parrinello says.
Remember that metadynamics adds the bias potential as a function of the CVs: fluctuations in those particular dimensions are enhanced, while fluctuations in all other dimensions are left as they are. So choosing the CVs for a system amounts to choosing which fluctuations to enhance. As such, even if they are not intended that way, different choices of CV can be seen as different hypotheses about the process under study. While the maths will take care of itself regardless, the challenge is to choose CVs to reflect the actual physics of a given process, Prof. Parrinello suggests: “Our choice of collective variables is where we put the physics back into the mathematics.”
The idea is put into practice in his and Mr Piaggi’s work on crystal formation. Crystallisation being a prime example of a barrier-crossing process that doesn’t fit the timescale of atomistic simulations, enhanced sampling techniques have been applied extensively in this area. However, Mr Piaggi says “The collective variables used for crystallisation typically include geometrical information, which prejudges the structure into which the system is going to crystallise. If you’re trying to discover new crystal structures, that rather defeats the purpose.”
It would be extremely useful, then, to have an enhanced sampling method that does not assume the final structure from the start: What happens, and what crystal structures emerge, if the crystallisation process is left to just play out from scratch, without being pushed in a particular direction? “The idea was to reproduce the crystallisation process on the computer, starting from the liquid phase and letting the system discover all the possible crystal structures.” Mr Piaggi explains.
Enhanced sampling is essential to this idea, or the timescale of crystallisation would keep it out of reach for atomistic simulations. But so is a clever choice of collective variables: if the idea is to mimic on a computer what happens in a real system, the CVs used to drive the simulation should reflect the physics of the actual process as faithfully as possible. To this end, the strategy was to go back to basics. As Mr Piaggi explains, “It came naturally to recall that equilibrium states tend to minimise the free energy ∆G = ∆H -T∆S (with G the free energy, H the enthalpy, S the entropy and T the temperature). In crystallisation, as in all first order transitions, this means there is a trade off between enthalpy and entropy. The idea was to use that interplay: introduce two CVs that describe those changes; then run a simulation and see what happens.”
That is exactly what Mr Piaggi and his co-authors did. They defined two CVs as surrogates for enthalpy and entropy. By enhancing the fluctuations in these two, they effectively created a time-lapse view of how the interplay between the two results in crystal formation. (See Video 1)
To demonstrate the potential of these CVs for polymorph screening, they then applied the method to urea — with promising results: in addition to all the known polymorphs of urea, they found a new one that has not been reported before (polymorph B in Fig. 2). The polymorph is particularly interesting because it is stabilised by strong entropic effects, Mr Piaggi points out: Compared to form I, form B has a relatively high enthalpy. Given that this is a crystal phase, it is counterintuitive that the entropy should be high enough to offset the enthalpy. Still, that is exactly what happens: the crystal features fast rotations around the molecules’ axis (as shown in Video 2), and this accounts for the high entropy, the authors calculated.
This result nicely illustrates the importance of the paper’s approach: constructing entropy and enthalpy as collective variables in a metadynamics simulation, the authors managed not just to identify (new) polymorphs but also to pinpoint which ones may be expected to show up at a given thermodynamic condition. Specifically, they managed to identify a crystal structure that is stabilised by entropy. “This shows that, counterintuitive as it may be, entropy can be a crucial stabilising factor, even in crystals. Given entropy’s association with disorder, it is often assumed that energy is all that matters for the stability of solid phases. But taking that approach, we would have missed this crystal,” Mr Piaggi stresses.
References
P. Piaggi and M. Parrinello, Predicting polymorphism in molecular crystals using orientational entropy, Proceedings of the National Academy of Sciences Sep 2018, 201811056; DOI:10.1073/pnas.1811056115
P. Piaggi, O. Valsson, M. Parrinello, Enhancing entropy and enthalpy fluctuations to drive crystallization in atomistic simulations, Physical Review Letters 119, 015701 (2017) DOI: 10.1103/PhysRevLett.119.015701
Low-volume newsletters, targeted to the scientific and industrial communities.
Subscribe to our newsletter