First principles physics from a Brazilian mine
by Fiorien Bonthuis, NCCR MARVEL
In 2008, in the Cauê mine in Brazil, miners discovered a new mineral (Figure 1). A minuscule, metallic grey speck in a piece of iron ore, they called it Jacutingaite, after the local term for the ore in which it was found. Little did the miners know that they had dug up a piece of pure theoretical physics: as a team of researchers from the EPFL THEOS lab shows, monolayer Jacutingaite realises the hitherto strictly theoretical Kane-Mele model for quantum spin Hall insulators.
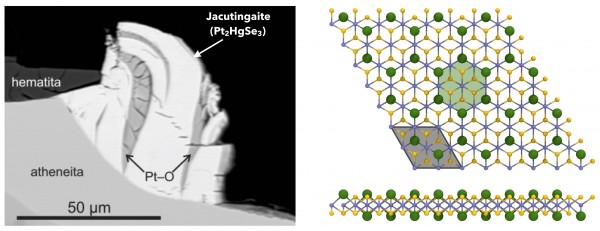
Figure 1: (Left) Back-scattered electron image of jacutingaite (white), on the surface of an aggregate of hematite, potarite and atheneite (adapted from Cabral et al., Terra Nova, 2008 and Vymazalová et al., The Canadian Mineralogist, 2012). (Right) Top and lateral views of monolayer jacutingaite (Pt2HgSe3)
In the most non-technical terms, what that means is that this exotic material hosts an exotic state of matter. To explain this, let’s start from the not-so exotic states of matter: solid, liquid, gas. Building on what happens in paradigmatic phase transitions such as water freezing to ice, the so-called Landau paradigm defines these phases (including less humdrum ones, such as ferromagnets and superconductors) in terms of a change in ordering for some property, and the associated breaking of some symmetry.
This paradigm breaks down, however, in 2D systems: here the appearance of long-range order and spontaneous symmetry-breaking are shown to be impossible. Accordingly, in the Landau paradigm, there can be no phases or phase transitions in 2D materials. This conclusion was refuted by work by David Thouless and Michael Kosterlitz in the early 1970s. They argued that in 2D systems there are phases, but of a different, topologically defined kind.
Kosterlitz and Thouless showed that a 2D vector field can have small topological excitations or vortices. A vortex is a topological defect. A single vortex cannot be transformed by continuous rotation to a configuration where all the vectors are aligned. A configuration with a vortex-antivortex pair, by contrast, can be so transformed. That is to say: the single-vortex and the vortex-pair configurations are topologically distinct states, but the vortex-pair configuration is topologically the same as the no-vortex state. In 2D systems, tightly bound vortex-antivortex pairs may form at low temperatures; as the temperature rises, these pairs split up and move away as single vortices. This would constitute a topological phase transition.
We can further characterise those phases with a topological invariant. A topological invariant is an integer quantity that stays the same under continuous deformations. Take the classic example that, from a topological point of view, a coffee cup is the same as a donut but different from a pretzel: here, the topological invariant is the number of holes. For vortices it is winding number, or the number of times they travel counterclockwise around a central point. Systems with the same topological invariant are in the same topological phase.
Discovery in this field is overwhelmingly driven by theory. All experimental realisations follow sharp theoretical predictions, often powered by atomistic simulations. But that means that often, we have the maths before we have the material.
— Antimo Marrazzo
All this yields a completely new paradigm for the study of phases of matter. It was soon recognised that the topological approach can be applied quite generally to different aspects of the quantum state. As it turns out, topologically non-trivial states are associated with all sorts of quantum effects in 2D systems and on surfaces. As these states may be realised in ordinary condensed matter, this holds great promise, both for fundamental research and for technological applications.
The catch? There aren’t a lot of known materials that exhibit a robust topological phase. “Discovery in this field is overwhelmingly driven by theory. All experimental realisations follow sharp theoretical predictions, often powered by atomistic simulations,” Antimo Marrazzo, lead author of the study says. “But that means that often, we have the maths before we have the material.”
This was the case with quantum spin Hall insulators. QSHIs are a theoretical spin-off of the quantum Hall effect, discovered in 1980 by Klaus von Klitzing. The quantum Hall effect arises when a strong magnetic field is applied perpendicularly to a two-dimensional electron system. As the magnetic field is gradually turned up, the transverse resistance (measured across the width of the plane) is quantised. At the same time, the longitudinal resistance (measured along the length of the plane) disappears. That is, the sample is insulating in the bulk, but conducting around the edges.
What is more, in measurements, the quantisation is extremely precise, and the effect is surprisingly robust against disturbances and impurities. This required explanation — which came from the topology of the quantum state. The idea is similar to the topological account of the vortices above, but more abstract, as we move from real space to momentum space. Specifically, what we need is a topological account of the electronic band structure. Constructing such an account is rather mathematically involved, but once we have it, we have all the tools we need.
To begin with, we can explain both the quantisation of the quantum Hall effect and its robustness: the Hall conductance can be construed as a topological invariant. Accordingly, the jumps are jumps between different topological phases, and therefore necessarily integer steps. The topological nature of the phase also explains its robustness: topological invariants are not destroyed by continuous, ‘stretching’-like disturbances.
Further, we can begin to explain the insulator/conductor duality. As is well known, the difference between insulators and conductors is that insulators have a gap in their electronic band structure separating the ground state from all excited states, whereas conductors don’t. Like an ordinary insulator, a topological insulator has a bulk band gap. Crucially, having a gap as opposed to no gap doesn’t mean all insulators are topologically equivalent. We can say that two insulators are topologically equivalent if we can transform one into the other by slowly changing the Hamiltonian, such that the system always remains insulating. A consequence of this is that connecting two topologically inequivalent insulators necessarily involves a phase transition, where the energy gap vanishes. In other words: at the edge there will be gapless, i.e. conducting, states.
But that is only the beginning. Just as insulating gapped states can be topologically distinct, so being gapless doesn’t mean all conducting edge states are topologically equivalent. “The cool thing here is the bulk-boundary correspondence,” Marrazzo explains. “There is a deep principle relating the topological invariants of the bulk to the electronic structure of the boundary. That is, the edge phenomena are completely determined by the topology of the bulk wave function.”
Thus, the topological theory of phases unlocked all sorts of topologically protected states of matter. In particular, it predicted the existence of topological insulators (Figure 2). Similar to the quantum Hall effect, these materials are insulating in the bulk but conducting around the edges — but without the external magnetic field. QSHIs are an example. They are essentially two copies of a quantum Hall system: they feature helical edge states where spin-up and spin-down electrons travel in opposite directions in separate lanes.
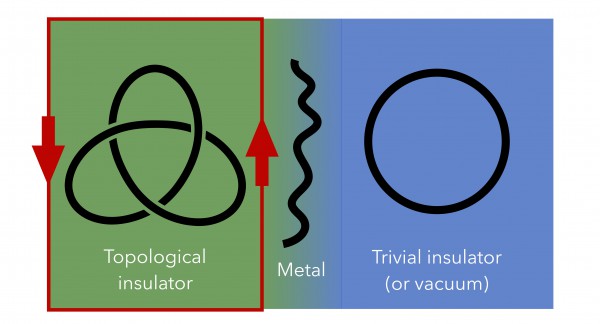
Figure 2: Schematic representation of a topological insulator.
The bulk-boundary correspondence allows us to calculate on a first principles basis whether a material might exhibit a quantum spin Hall phase. Thus, in 2005, Charles Kane and Eugene Mele predicted that graphene could host a QSHI, but experimentally, the effect is too small to observe. Soon after, QSHIs were experimentally confirmed, but in HgTe quantum wells rather than graphene. These QSHIs are driven by a band inversion mechanism, while the Kane-Mele’s graphene model relies on a spin-orbit energy gap. QSHIs of the Kane-Mele type remained elusive.
From a NCCR MARVEL point of view, that is an unsatisfactory state of affairs: Couldn’t there be a material that is enough like graphene to host a QSHI of the Kane-Mele type, but unlike it enough to make the effect measurable?
Enter another MARVEL project: the 2D materials database. Constructed by Nicolas Mounet and Marco Gibertini, this database contains close to 2000 materials that may be exfoliated to 2D materials. Using computer simulations, Marrazzo scanned the database for 2D materials that might host the quantum spin Hall phase — and found Jacutingaite. “Monolayer Jacutingaite did not look like the other QSHIs, and it immediately reminded me of the Kane-Mele prediction,” Marrazzo says.
The researchers performed first principles calculations to show that the topological physics of monolayer jacutingaite satisfies the same mathematics as Kane and Mele’s graphene-based model. Moreover, jacutingaite turned out to have additional attractive properties.
Firstly, jacutingaite has a much larger bulk gap than graphene (Figure 3). This makes the measurable effect of the topological state stronger. The authors suggest that this large band gap should facilitate experimental detection of the QSHI state. Secondly, Jacutingaite’s crystal structure is more complex than graphene’s. This allows for a richer physics, driven by spin-orbit coupling. The authors show how, thanks to this additional complexity, the QSHI phase in jacutingaite is switchable (Figure 3): applying an out-of-plane electric field drives the material into an ordinary insulating phase. This means that we can manipulate the phase behaviour, switching it on and off.
All this makes jacutingaite a theoretically interesting and practically potentially useful quantum spin Hall insulator. Without MARVEL, the miners might never have known what an exciting piece of physics they had found.
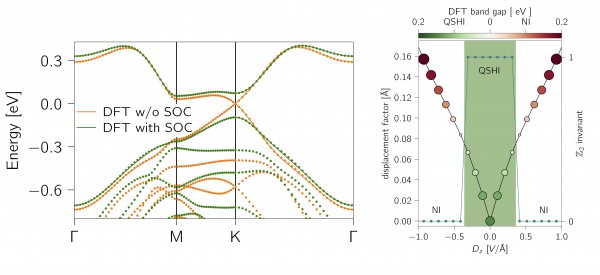
Figure 3: (Left) DFT band structures, showing the band gap opening driven by spin-orbit coupling. (Right) Topological phase diagram under an out-of-plane electric displacement field Dz, showing the switchable QSHI phase.
Reference
Antimo Marrazzo, Marco Gibertini, Davide Campi, Nicolas Mounet, and Nicola Marzari, Prediction of a Large-Gap and Switchable Kane-Mele Quantum Spin Hall Insulator, Phys. Rev. Lett. 120, 11 (2018). doi: 10.1103/PhysRevLett.120.117701
Contact
Nicola Marzari: nicola.marzari@epfl.ch
Theory and Simulation of Materials (THEOS) and National Centre for Computational Design and Discovery of Novel Materials (MARVEL), École Polytechnique Fédérale de Lausanne, 1015, Switzerland.
Low-volume newsletters, targeted to the scientific and industrial communities.
Subscribe to our newsletter