A new tool for discovering nanoporous materials
Fiorien Bonthuis, EPFL, NCCR MARVEL
Smit et al. have developed an innovative method that builds on techniques from topological data analysis (persistent homology). They show that this method is effective at identifying materials with similar pore geometries. Moreover, in a case study of materials for methane storage, they show that we can find materials that perform as well as known top-performing materials by searching the database for materials with similar pore shapes; conversely, they show that the pore shapes of the top-performing materials can be sorted into topologically distinct classes, and that materials from each class require a different optimisation strategy.
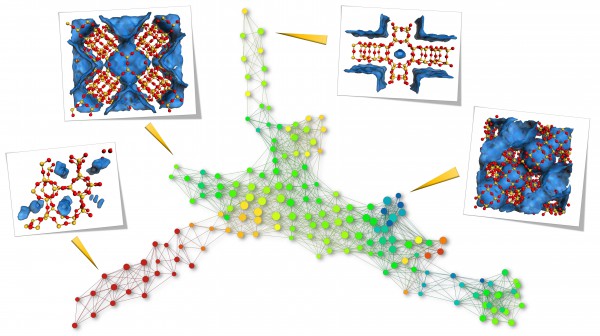
Topological differences of top-performing materials for methane storage. Topological data analysis reveals the similarity between structures; each node represents a family of similar materials, while a network between two nodes indicates that they share at least one material. The further apart the nodes are, the more dissimilar the materials. The pictures show examples of nanoporous materials at the edges, and represent the topologically most different materials (red = Si, yellow = O, blue area = Pores).
Credit: Berend Smit/EPFL | Figure obtained with the Ayasdi Core software platform
For the longest time, materials discovery was mostly a matter of intuition and serendipity: with insight and a bit of luck, long hours in the lab might eventually result in the discovery of a material with just the properties we were looking for. With the advent of computers and big data science, this has changed. Instead of making and testing new materials one by one, we can now use computers to screen large databases of (potential) materials, and determine — before synthesis — which materials would perform best for a given application.
One class of materials for which screening methods promise to be especially fruitful are nanoporous materials, such as zeolites or metal organic frameworks (MOFs), with applications ranging from gas separation and storage to catalysis. Their chemistry is so versatile that the number of new materials we can obtain is virtually unlimited. The challenge, of course, is to actually find the best material among those millions of possibilities. Here, big data methods are the only viable option, Prof. Smit argues.
The success of big data methods for materials discovery stands or falls, however, with our ability to screen databases for the right properties, i.e. for those properties that determine performance. Now, for most applications of nanoporous materials, pore shape is as important a predictor of performance as chemical composition. So, for many applications, finding the best nanoporous material means finding materials with pore shapes that are optimal for a given application. The problem? But while it is easy for a human to decide whether two structures look alike or how different their shape is, it was not known how to quantify and compare similarity in pore shape. Consequently, there was no adequate method to screen databases by pore shape.
Pore shape is conventionally characterized in terms of geometric descriptors such as pore volume, surface area, etc. While these descriptors can be optimized to search for materials with similar overall thermodynamic properties, they do not encode enough geometric information to detect materials with similar overall pore shapes. As this is essentially a mathematical problem, Prof. Smit assembled a team that includes mathematicians as well as theoretical chemists. They developed a method to quantify the geometric similarity of pore structures using topological data analysis — a field of big data analysis that builds on techniques from algebraic topology, specifically in this case, persistent homology. The method yields "fingerprints", represented by barcodes, that characterize the pore shapes of each material in the database (see figure and text at the bottom of the page). We can compare these fingerprints to compute how similar the pore shapes of two materials are.
The most elementary application of this approach is, of course, screening databases to identify materials with similar pore structures. To test this, the MARVEL team took a reference structure and searched the database for similar pore shapes, once using the topological method, and once using conventional descriptors. The topological approach is very successful at finding structures that really look similar to the original.
So the method "does what it says on the tin", and that already is an important and non-trivial achievement. As Prof. Smit explains, "We have a database of over 3'000'000 nanoporous materials, so finding similar structures through visual inspection is out of the question. In fact, going through the literature, we found that authors often don’t realize when a new MOF has the same pore structure as another one. So we really need a computational method. However, while humans are intuitively good at recognizing shapes as the same or different, it is quite difficult to get a computer to emulate this skill."
The team goes on to show how the method can help materials discovery in a case study of materials for methane storage. They show, firstly, how searching the database for materials with pore shapes similar to known top-performing materials can help us find further top-performing materials. Secondly, they show that distinguishing the top-performing materials by pore shape can help us improve our optimisation strategies: different classes of pore topologies require different strategies.
Thus, the case study underscores just how critical pore shape is as a factor to be taken into account in nanoporous materials discovery — and how the new method to quantify similarity of pore geometry can greatly accelerate materials discovery in the lab.
This work was a collaboration between researchers at EPFL in Switzerland, INRIA in France and UC Berkeley in the USA.
Reference
Yongjin Lee, Senja D Barthel, Paweł Dłotko, S Mohamad Moosavi, Kathryn Hess and Berend Smit, Quantifying similarity of pore-geometry in nanoporous materials, Nature Communications 8, 15396 (2017)
doi: 10.1038/ncomms15396
Persistence homology | Examples of zeolite fingerprints
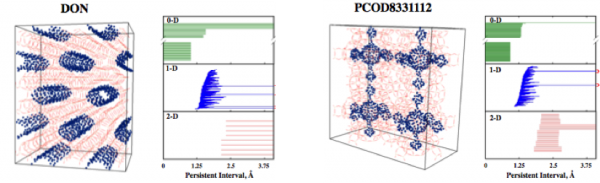
To compute the fingerprints, first, we encode the material (red network, above) as a point cloud, by sampling points on the pore surface (blue dots, above). These points are grown as balls with increasing radius. They form a growing geometric object as they overlap, called simplicial complex, whose topology we analyse while it grows. Namely, we are computing the 0-, 1-, and 2- dimensional homology classes of the simplicial complex. This is the mathematical way of counting the number of clusters, the number of circles and the number of pockets and tunnel in the geometric object that appears when the sampled points are thickened.
From this, second, we construct a so-called filtered Vietoris-Rips complex, which we characterize in terms of its 0- (green), 1- (blue), and 2-dimensional (red) homology classes. While the homology classes of the point cloud itself are not very informative, the homology classes of the associated Vietoris-Rips complex strongly depend on the position of the points in space.
Third, we represent each homology class (corresponding to either a cluster, a circle, or a cavity) by an interval with start point the radius of the balls when they first touch to form the homology class and endpoint the radius of the balls when the object disappears; for example when the points forming a circle have grown so large, that they all touch and the whole of the circle is filled in. We store this information in persistence barcodes, which track the lifetime of each non-trivial homology class in the Vietoris-Rips complex: each homology class is represented by a bar; its starting point denotes the smallest radius for which the homology class appears, and its end point the radius where the homology class disappears. Homology classes that persist through long intervals reveal structural features of the point cloud.
Finally, for each dimension, we form a barcode by combining the intervals tracing the homology classes of this dimension. The 0-, 1-, and 2- dimensional barcodes together yield a fingerprint that characterizes the overall shape of the pore structure.
Low-volume newsletters, targeted to the scientific and industrial communities.
Subscribe to our newsletter